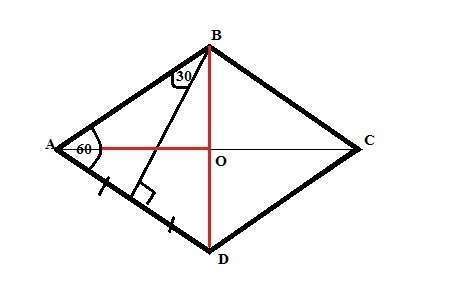
Дано: ромб АВСD, высота ВН, АН=НD=(1/2)*а, где "а" - сторона ромба.
В ромбе против большей диагонали лежит тупой угол.
Тогда в треугольнике АВН угол АВН=30°, так как катет АН равен половине гипотенузы АВ. Угол ВАН=60° (сумма острых углов прямоугольного треугольника равна 90°), а это угол А ромба.
Следовательно, треугольник АВD - равносторонний, а его высота АО (О - точка пересечения диагоналей) равна половине диагонали АС, то есть АО=2√3.
Формула высоты: h=(√3/2)*a, отсюда сторона а=2h/√3 или а=4√3/√3=4см.
Площадь ромба равна S=a²*SinA или S=16*√3/2 =8√3 см².
Или так:
поскольку диагональ ВD равна стороне ромба (доказано выше), то его площадь равна S=(1/2)*D*d или S=(1/2)*4√3*4=8√3 см².
Ответ: S=8√3 см².