Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
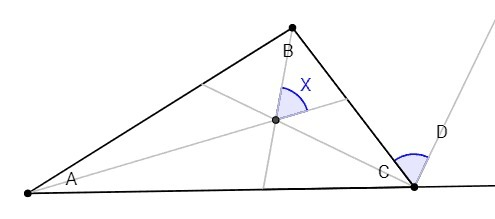
D= A +B
X= A/2 +B/2
Биссектрисы внутреннего (С) и внешнего (D) углов перпендикулярны.
D/2= 90 -С/2
X= (A+B)/2 = D/2 = 90 -С/2
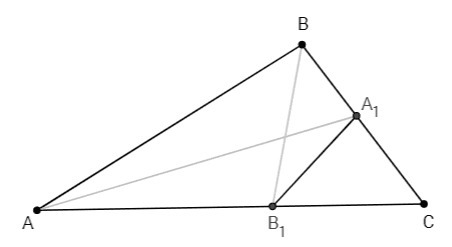
Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
AB1/B1C = AB/BC
AC= AB1 +B1C <=> AC= AB*B1C/BC +B1C <=> B1C= AC*BC/(AB+BC) =24/11
Аналогично A1C= BC*AC/(AB+AC) =24/9
AB^2= AC^2 + BC^2 -2*AC*BC*cos(C) <=> cos(C) =9/16
sin(C)= √(1 -cos^2(C)) =5√7/16
SA1CB1= A1C*B1C*sin(C)/2 =10√7/11
SACB= AC*BC*sin(C)/2 =15√7/4
SABA1B1= SACB -SA1CB1 =125√7/44 =7,52