Хорошо, в принципе без рисунка можно вывести ответ формулами.
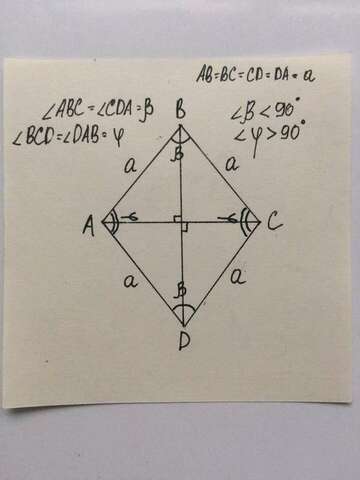
Решение (см.Рисунок во вложении): ∠β ²±√
1)Из теоремы косинусов найдем меньшую диагональ АС, лежащую напротив угла ∠β:
АС² = АВ² + ВС² - 2*АВ*ВС*cosβ
АС = √(АВ² + ВС² - 2*АВ*ВС*cosβ), где АВ² = а², ВС² = а².
имеем АС = √(а²+а²-2*а*а*cosβ)
AC = √(2a² - 2a²*cosβ) = a√(2(1 - cosβ))
2)Назовем тупой угол ромба - γ , γ = 180° - β
Из теоремы косинусов найдем большую диагональ ВD, лежащую напротив угла ∠γ:
ВD² = CD² + ВС² - 2*CD*ВС*cosγ
ВD = √(CD² + ВС² - 2*CD*ВС*cosγ), где CD² = а², ВС² = а².
имеем ВD = √(а²+а²-2*а*а*cosγ)
ВD = √(2a² - 2a²*cosγ) = a√(2(1 - cosγ)).
Вот собственно и все
меньшая диагональ ромба АС = a√(2(1 - cosβ))
большая диагональ ромба ВD = a√(2(1 - cosγ)).
Ответ: a√(2(1 - cosβ)) ; a√(2(1 - cosγ)).