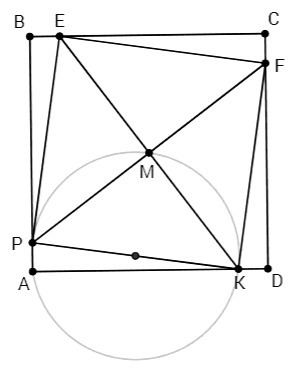
1) У квадрата все углы прямые и все стороны равны.
AP=BE=CF=DK => PB=EC=FD=KA (вычитаем из равных длин равные).
Прямоугольные треугольники, отсекаемые отрезками PE, EF, FK, KP, равны по двум катетам => их гипотенузы равны => PEFK - ромб (все стороны равны).
Диагонали ромба пересекаются под прямым углом. PF⊥EK
∠AKP+∠APK=90 (сумма острых углов прямоугольного треугольника)
∠AKP=∠BPE
∠KPE= 180-∠BPE-∠APK =90
Ромб PEFK является квадратом, т.к. один из его углов (∠KPE) прямой.
Площадь квадрата равна половине квадрата диагонали.
SPEFK= EK^2/2 = 10^2/2 =50
(Площадь выпуклого четырехугольника равна половине произведения диагоналей и синуса острого угла между ними. Диагонали квадрата равны и пересекаются под прямым углом. sin90=1).
2) Площадь квадрата равна квадрату стороны.
SPEFK= PK^2 =50
По теореме Пифагора:
AK= √(PK^2 -AP^2) = √(50-1) =7
AD= AK+DK = 7+1 =8
3) ∠PAK=90 (у квадрата ABCD все углы прямые)
∠PMK=90 (диагонали квадрата PEFK пересекаются под прямым углом)
Т.к. в четырёхугольнике APMK сумма двух противоположных углов (∠PAK, ∠PMK) равна 180, то около него можно описать окружность.
4) Вписанный прямой угол опирается на диаметр. ∠PAK=90 => PK - диаметр окружности, описанной около APKM.
R= PK/2 = √50/2 = 5√2/2 (~3,54)