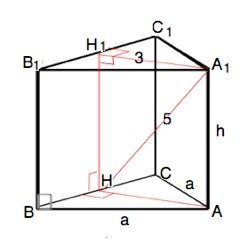
В основании правильной треугольной призмы – равносторонний треугольник, все грани – прямоугольники и перпендикулярны основанию.
Расстоянием от вершины А1 до противоположной плоскости является длина проведенного перпендикулярно к ней отрезка. Он лежит в плоскости основания, так как грани и основания взаимно перпендикулярны. Это высота А1Н1 основания А1В1С1.
Расстояние от точки до прямой - длина отрезка, проведенного к ней перпендикулярно.
По т. о 3-х перпендикулярах это А1Н, проекция которой перпендикулярна стороне ВС в её середине.
НН1 - высота призмы. ∆ А1Н1Н= египетский, – НН1=4 (проверьте по т.Пифагора).
Площадь полной поверхности призмы - сумма площади 2-х оснований и всех боковых граней.
S=2•Sосн+Sбок
Формула площади основания правильного треугольника
S=а²√3:4
a=AB=AH:sin60°=3:√3/2=2√3
S(осн)=12√3:4=3√3
S(бок)=h•P=4•3•2√3=24√3
S(полн)=2•3√3+24√3=30√3