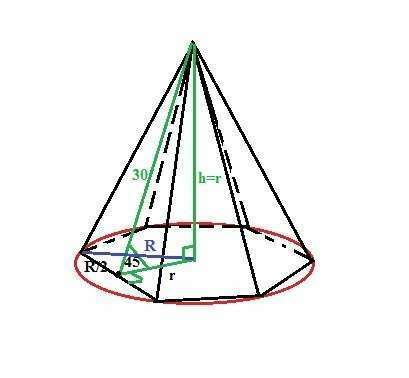
Высота пирамиды равна радиусу вписанной окружности, так как апофема наклонена к основанию под 45°, а вписанная окружность касается середины стороны правильного шестиугольника.
Итак, h=r, тогда по Пифагору 2r²=30², r=√450=15√2см.
В правильном шестиугольнике сторона равна радиусу описанной окружности. Тогда по Пифагору R²-R²/4=r² или 3R²=1800, отсюда
R=√600=10√6 см. Это ответ.