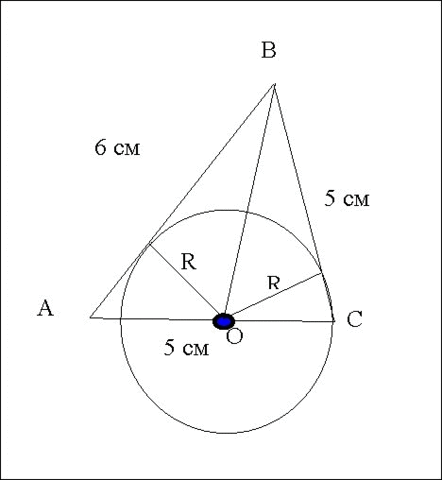
Дано: ∆АВС
АВ = 6 см
ВС=АС=5 см
центр полуокружности О ϵ АС
R – радиус полуокружности
π = 3
Найти L – длину полуокружности
Решение
1) Найдём площадь S ∆АВС
по формуле Герона.
S = √(p(p-a)(p-b)(p-c))
p =
(6+5+5)/2=8cм
S = √(8(8-6)(8-5)(8-5))
= √(8*2*3*3)= √(16*9)=4*3=12 см²
S = 12 cм²
2) Найдём площадь S ∆АВС
через сумму площадей ∆АВО и ∆ВОС
У этих треугольников радиус R, проведённый к точке касания всегда
перпендикулярен касательной, а значит, R является высотой.
Для ∆АВО площадь S₁ = ½*AB*R
Для ∆ВОC
площадь S₂ = ½*BC*R
Найдём площадь S ∆АВС
S = S₁ + S₂
S = ½*AB*R+ ½*BC*R = ½ *R(AB+BC)
S = ½ *R(AB+BC)
Выразим R:
R =
2S/(AB+BC)
R = 2*12/(6+5)
= ²⁴/₁₁ см
3) Наконец находим L= С/2 =2πR/2=
πR
L = πR
L = 3* ²⁴/₁₁= ⁷²/₁₁ = 6 ⁶/₁₁ ≈6,5 см
Ответ: L≈ 6,5 см