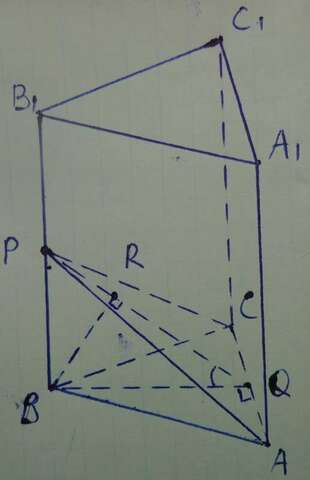
Снования призмы всегда параллельны, поэтому тангенс угла между плоскостями (А₁В₁С₁) и (ACP), который нужно найти, равен тангенсу угла между плоскостями (АВС) и (ACP), который будем искать.
Угол плоскостями (АВС) и (ACP) -- это ∠BQP, где BQ -- высота Δ АВС.
Высота BQ равнобедненного Δ АВС является ещё и медианой, поэтому АQ = АС/2 = 16/2 = 8.
По теореме Пифагора: BQ = \sqrt{AB^2-AQ^2}= \sqrt{10^2-8^2}=6.
По условию BP = BB₁/2 = 24/2 = 12.
tg∠BQP = BP/BQ = 12/6 = 2
Расстоянием от точки B до плоскости (APC) будет перпендикуляр BR.
BR = BQ*sin\ \textless \ BQP = BQ* \sqrt{1-cos^2\ \textless \ BQP}= =BQ* \sqrt{1- \frac{1}{1+tg^2\ \textless \ BQP}}=BQ* \sqrt{\frac{tg^2\ \textless \ BQP}{1+tg^2\ \textless \ BQP}}=BQ* \frac{tg\ \textless \ BQP}{\sqrt{1+tg^2\ \textless \ BQP}}==6*\frac{2}{\sqrt{1+2^2}}=\frac{12}{\sqrt5}=\frac{12\sqrt5}{5}.
Приложение