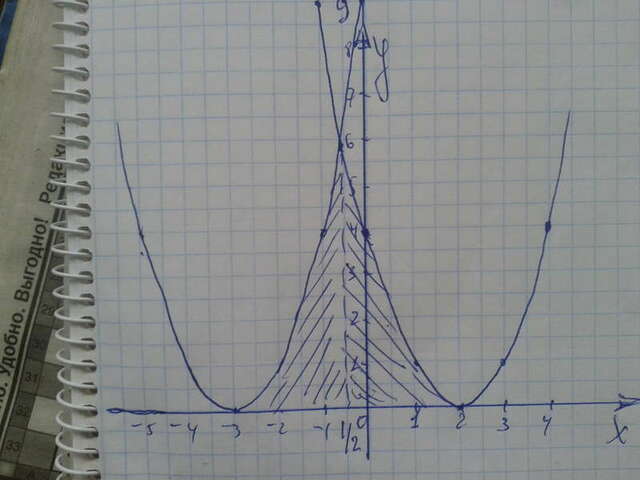
Y=x²-4x+4 y=x²+6x+9 y=0 S=?
x²-4x+4=0 (x-2)²=0 x-2=0 x=2
x²+6x+9 (x+3)²=0 x+3=0 x=-3
x²-4x+4=x²+6x+9
10x=-5
x=-0,5
S=S₁+S₂=₋₃∫⁻⁰`⁵(x²+6x+9)dx+₋₀,₅∫²(x²-4x+4)dx
S₁=(x³/3+3x²+9x) |⁻⁰`⁵₋₃=-(1/8)/3+0,75-4,5-(-9+27-27)=
=-1/24-3,75+9=5,25-1/24.
S₂=(x³/3-2x²+4x) |²₋₀,₅=8/3-8+8-(-(1/8)/3-0,5-2)=8/3+1/24+2,5
S=5,25-1/24+8/3+1/24+2,5=7,75+8/3=7³/₄+8/3=31/4+8/3=125/12
Ответ: S=125/12≈10,42 кв.ед.