11 - Три станка
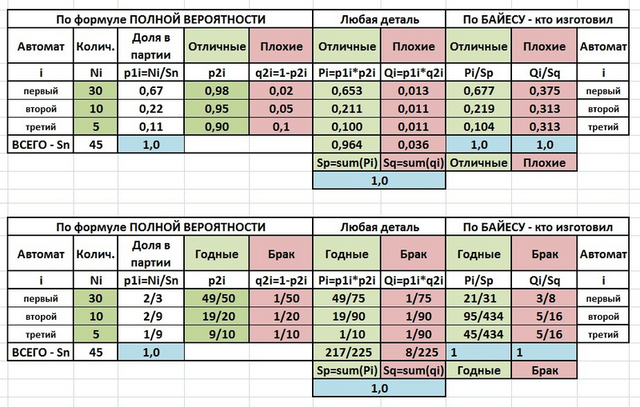
Расчет сведен в таблицу в приложении.
Событие А состоит из двух независимых событий - взять случайную деталь - Р1 и взять бракованную деталь - Р2.
Делаем расчет вероятности Р1 по данным - Ni
P11 = 30/45 = 2/3 и P12 = 10/45 = 2/9 и P13 = 5/45 = 1/9. - это вероятность любой случайной детали.
Вероятности брака - даны - это - q2i.
Выраженная в дробях будет
q21 = 0.02 = 1/50 и q22 = 0.05 = 1/20 и q23 = 0.1 = 1/10.
Вероятность И случайная И бракованная ИЛИ первого ИЛИ второго ИЛИ третьего - сумма произведений вероятностей.
Вычисляем для БРАКА
Sq = p11*q11 + p12*q12 + p13*q13 = 1/75 + 1*90 + 1*90 = 8/225 ≈ 0,036 ≈ 3,6% - это вероятность того, что случайная деталь бракованная.
Дополнительно - можно увидеть, что вероятность случайной годной детали - Sp=217/225 ≈ 0.964≈ 96.4%
По формуле полной вероятности - сумма таких вероятностей равна 1
Теперь по формуле Байеса находим вероятность на каком станке она сделана..
Q1/Sq = 1/75 : 8/225 = 3/8 ≈ 0,375 ≈ 37,5% - для первого станка.
Для двух других станков - вероятности одинаковые - 5/16 ≈ 0,313 ≈ 31,3%.
ОТВЕТ
а) вероятность брака - 3,6%
б) наиболее вероятно, что сделана на первом станке (37,5%)
11. Две партии деталей.
Вероятности для первой партии - p1 = 7/10 и q1= 3/10 (брак)
Для второй партии - p2 = 10/14 = 5/7 и q2 = 2/7 (брак)
Вопрос 1 - обе детали годные - событие "И" - произведение вероятностей.
Р(А) = p1 * p2 = 7/10 * 5/7 = 1/2 = 0.5 = 50% - обе годные - ОТВЕТ
Вопрос 2 - первая годная И вторая брак
Р(А) = p1 * q2 = 7/10 * 2/7 = 1/5 = 0,2 = 20% - ОТВЕТ