Область определения и область значений:
D(y)=(-\infty,+\infty)D(y)=(−∞,+∞) - функция определена на всей вещественной оси х.
E(y)=(-\infty,+\infty)E(y)=(−∞,+∞) - значения функции определены на всей вещественной оси у.
Четность,нечетность функции:
Функция чётна, если выполняется условие:
f(x)=f(-x)f(x)=f(−x)
Функция не чётна, если выполняется условие:
f(-x)=-f(x)f(−x)=−f(x)
2(-x)-2=-2x-22(−x)−2=−2x−2 - следовательно, наша функция не четная, не нечетная.
Точки пересечения с осями:
y=2*0-2 \Rightarrow y=-2y=2∗0−2⇒y=−2 -> (0,-2)
0=2x-2 \Rightarrow x=10=2x−2⇒x=1 -> (1,0)
Экстремумы и интервалы монотонности:
Производная :
(2x-2)'=2(2x−2)′=2
2 Не может равняться нулю. Следовательно не существует экстремумов у данной функции.
2 \geq 02≥0 - следовательно функция постоянно растет.
Интервалы знакопостоянства:
Функция определена на всей вещественной оси х.
Находим нули функции:
2x-2=0 \Rightarrow x=12x−2=0⇒x=1
Отсюда имеем 2 интервала:
\begin{lgathered}(-\infty,1) \\2x-2 \Rightarrow -\end{lgathered}(−∞,1)2x−2⇒−
\begin{lgathered}[1,+\infty) \\2x-2\Rightarrow +\end{lgathered}[1,+∞)2x−2⇒+
Следовательно:
\begin{lgathered}f(x)\ \textless \ 0 \rightarrow (-\infty,1) \\f(x) \geq 0 \rightarrow [1,+\infty)\end{lgathered}f(x) < 0→(−∞,1)f(x)≥0→[1,+∞) <br>
Так же заметим, что наша функция линейна, так как представима в виде:
f(x)=ax+bf(x)=ax+b
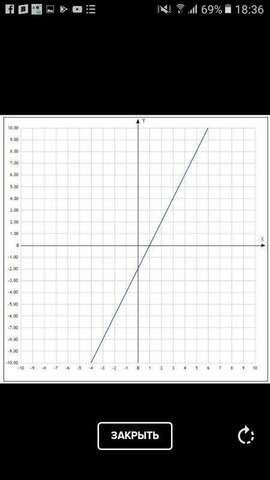
Следовательно, ее график является обычная прямая.
График во вложении.