ДАНО
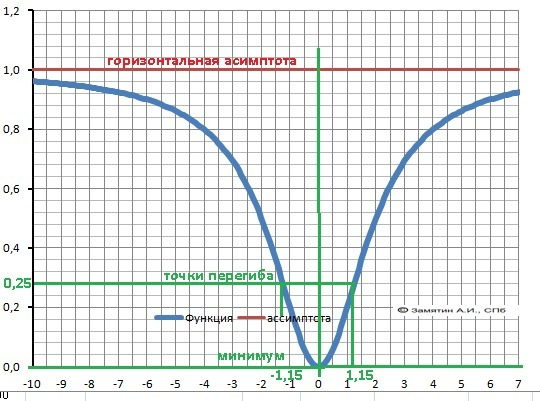
Y = x²/(x² + 4)
ИССЛЕДОВАНИЕ
1.Область определения D(x) - непрерывная Х∈(-∞;+∞).
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y=0 при х = 0.
3. Пересечение с осью У. У(0) = 0.
4. Поведение на бесконечности.

limY(+∞) = 1.
Горизонтальная асимптота - Y = 1.
5. Исследование на чётность.Y(-x) = Y(x).
Функция чётная.
6. Производная функции.

Корень при Х=0. Схема знаков производной.
(-∞)__(<0-убыв)__(х=0)_(<0-убыв)__(+∞)</p>
7. Локальные экстремумы.
Максимума - нет, минимум – Ymin(0) = 0.
8. Интервалы монотонности.
Убывает - Х∈(-∞;0]. Возрастает - Х∈[0;+∞)
9. Вторая производная - Y"(x).

Корни производной - точки перегиба: х1 =-2√3/3, х3= 2√3/3. (≈1,15)
9. Выпуклая “горка» Х∈(-∞;-2√3/3)∪(2√3/3;+∞),
Вогнутая –
«ложка» Х∈(-2√3/3;2√3/3).
10. Область значений Е(у) У∈(-∞;1)
11. График в приложении