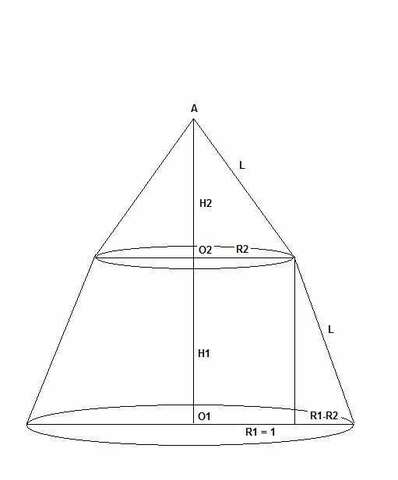
Я долго думал, как они расположены и, наконец, понял.
Образующие обозначим L, они одинаковые.
Суммарная высота O1O2 + O2A = H1 + H2 = 2
Большой радиус усеченного конуса R1 = 1.
1. a) Если R2 = 0,9, то в усеченном конусе
L^2 = H1^2 + (R1-R2)^2 = H1^2 + (0,1)^2 = H1^2 + 0,01
H1 = √(L^2 - 0,01)
V1 = 1/3*pi*H1*(R1^2 + R1*R2 + R2^2) =
= 1/3*pi*√(L^2-0,01)*(1^2+1*0,9+0,9^2) =
= 1/3*pi*√(L^2-0,01)*(1+0,9+0,81) = 2,71/3*pi*√(L^2-0,01)
А в полном конусе
L^2 = H2^2 + R2^2 = H2^2 + (0,9)^2 = H2^2 + 0,81
H2 = √(L^2 - 0,81)
V2 = 1/3*pi*H2*R2^2 = 1/3*pi*√(L^2-0,81)*(0,9)^2 = 1/3*pi*√(L^2-0,81)*0,81
Общий объем равен
V = V1 + V2
б) Если H1 = H2 = H, то в усеченном конусе
L^2 = H^2 + (R1-R2)^2 = H^2 + (1-R2)^2
R2 = 1 - √(L^2 - H^2)
V1 = 1/3*pi*H*(R1^2 + R1*R2 + R2^2) = 1/3*pi*H*(1 + 1*R2 + R2^2)
А в полном конусе
L^2 = H^2 + R2^2
R2 = √(L^2 - H^2)
V2 = 1/3*pi*H*R2^2 = 1/3*pi*H*(L^2 - H^2)
Приравниваем R2
1 - √(L^2 - H^2) = √(L^2 - H^2)
2*√(L^2 - H^2) = 1
√(L^2 - H^2) = 1/2 = R2
Подставляем
V1 = 1/3*pi*H*(1 + 1*R2 + R2^2) = 1/3*pi*H*(1 + 1*1/2 + 1/4) = 7/12*pi*H
V2 = 1/3*pi*H*R2^2 = 1/3*pi*H*1/4 = 1/12*pi*H
Общий объем
V = V1 + V2 = 7/12*pi*H + 1/12*pi*H = 8/12*pi*H = 2/3*pi*H
2. Границы - не знаю, как оценить.
3. Верхнее основание имеет стороны 5, 5, 6, P = 5 + 5 + 6 = 16
Высота этого треугольника h1 = √(5^2 - 3^2) = 4 см
Площадь S1 = 6*4/2 = 12 кв.см.
Нижнее основание имеет P = 32, и оно подобно верхнему.
Значит, это тоже равнобедренный тр-ник со сторонами 10, 10, 12.
Его площадь S2 = 4S1 = 12*4 = 48 кв.см.
Высота пирамиды H = 4 см. Объем пирамиды
V = 1/3*H*(S1 + √(S1*S2) + S2) = 1/3*4*(12 + √(12*48) + 48) =
= 1/3*4*(60 + √576) = 1/3*4*(60 + 24) = 1/3*4*84 = 4*28 = 112 куб.см.