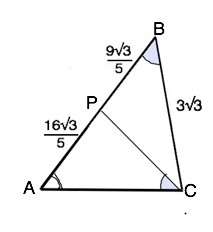
Сторона ВС треугольника АВС равна 3√3. На стороне АВ отмечена точка Р так, что угол АВС=углу АСР. Найдите площадь треугольника АВС, если

Для нахождения площади воспользуемся формулой
S=a•b•sinα:2, где α - угол между АВ и ВС.
Найдем синус∠α.
В треугольниках АВС и АВС угол А - общий, угол АСР=АВС. ⇒
∆ АВС~∆ АРС по двум углам.
Из подобия следует отношение
АС/АВ=ВС/АС ⇒ АС²=АВ•ВС

АС*=5√3•3√3=45
По т.косинусов
АС²=АВ²+ВС²-2•AB•BC•cosα
45=75+27-2•45•cosα
-102=-90•cosα
cosα=57/90=19/30
 ⇒
⇒