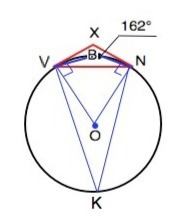
Поскольку угол VBN тупой, точка В расположена на меньшей дуге MN.
Отметим на большей дуге точку К и соединим её с M и N.
Четырехугольник KMNB вписанный, и по свойству вписанных четырехугольников сумма его противоположных углов равна 180°.
∠VКN=180°-162°=18°. Центральный угол, опирающийся на ту же дугу VBN, вдвое больше угла VКN и равен 36°.
Радиус, проведенный в точку касания, перпендикулярен касательной. ⇒ В четырехугольнике VXNO углы при V и N прямые, а сумма всех углов четырехугольника равна 360°. Поэтому сумма углов при его вершинах Х и О равна 360°- 2•90°=180°.
Отсюда ∠VXN= 180°-36°=144°