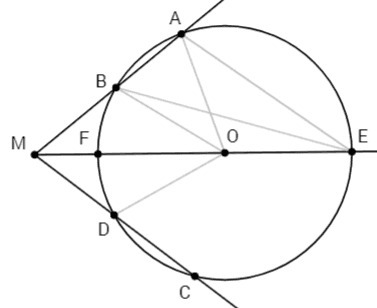
1) Теорема о секущих:
MA*MB=MC*MD
AB=CD <=> MA-MB=MC-MD
MA=a, MB=b, MC=c, MD=d
{ab=cd <=> a=cd/b
{a-b=c-d <=> a+d=c+b
{a=cd/b
{cd/b +d=c+b <=> d(c+b)/b=c+b <=> b=d
MB=MD, OB=OD => △MBO=△MDO (по трем сторонам) => ∠AME=∠CME
2) MA*MB=ME*MF <=> ME= MA*MB/MF =9*5/3 =15
r= FO/2 = (ME-MF)/2 =(15-3)/2 =6
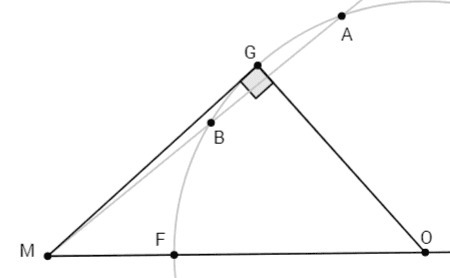
3) ∠MGO=90 (угол между радиусом и касательной)
По теореме Пифагора:
MO^2=OG^2 +MG^2 <=> MG= √[(MF+r)^2 -r^2] = √[(3+6)^2 -6^2] =3√5 (~6,7)
4) По теореме косинусов (△AOB):
AB^2= AO^2 +BO^2 -2*AO*BO*cos(AOB) <=>
cos(AOB)= (2r^2 -AB^2)/2r^2 = 1 -4^2/2*6^2 =7/9
arccos(7/9) = 38,94
Центральный угол равен мере дуги, на которую опирается (U AB). Величина вписанного угла (∠AEB) равна половине центрального (∠AOB), опирающегося на ту же дугу (U AB).
∠AEB= ∠AOB/2 = 38,94/2 = 19,47