1) Объем куба можно найти по формуле V=a³.
Отсюда находим сторону a=∛V=∛30 см.
Ответ: ∛30 см.
2) Пусть АВС - треугольник со сторонами АВ=13 см, ВС=14 см и АС=15 см.
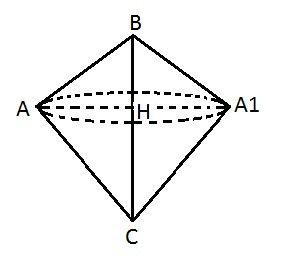
При вращении треугольника вокруг средней стороны ВС получается два конуса с общим основанием. (См. рисунок)
Поэтому объем полученной фигуры можно найти по формуле
1) V=V1+V2, где V1 - объем меньшего конуса, V2 - объем большего конуса.
V1=1/3*Sосн*h1;
V2=1/3*Sосн*h2;
V=1/3*Sосн*h1+1/3*Sосн*h2=1/3*Sосн(h1+h2)=1/3*Sосн*BC=1/3*Sосн*14=
=14/3*Sосн. (1)
2) Площадь основания (круга) можно найти по формуле:
Sосн=πR².
Радиусом основания является высота АН треугольника АВС.
Можно применить метод площадей: сначала найти площадь ΔАВС по формуле Герона, а затем из общей формулы площади треугольника найти высоту.
Формула Герона:
S=√(р(р-а)(р-b)(p-c)), где р - полупериметр треугольника, a, b, c - стороны треугольника:
p=(AB+BC+AC)/2=(13+14+15)/2=21 (см).
S=√(21(21-13)(21-14)(21-15))=√(21*8*7*6)=√(4²*7²*3²)=4*7*3=84 (см²).
Общая формула нахождения площади треугольника:
S=1/2*a*h=1/2*BC*AH=1/2*14*AH=7*AH;
7*AH=84;
AH=84/7=12 (см).
R=AH=12 см.
3) Находим площадь основания и поставляем в формулу объема (1):
Sосн=π*12²=144π (см²);
V=14/3*144π=672π (см³).
Ответ: 672π см³.