У кулі, об'єм якої 36п см3 проведено переріз. Радіус кулі, один з кінців якої належить...

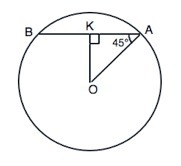
На схематическом рисунке АВ - диаметр сечения, ОА - радиус шара, ОК - расстояние от центра шара до плоскости сечения, т.е. до центра круга, образованного сечением.

Формула объёма шара $V= \frac{4 \pi R ^{3} }{3}$

$\frac{4 \pi R^{3} }{3}=36 \pi$ ⇒

R=3 см

Расстояние от центра шара до плоскости сечения - длина перпендикулярного отрезка, проведенного из центра шара к его диаметру. Диаметр сечения - хорда, ОК - перпендикуляр из центра шара к хорде, поэтому делит АВ пополам. АК=ВК=r сечения.

∆ АОК- прямоугольный.

АК=АО•sin45°=3•√2/2=1,5√2

S=πr²=π(1,5√2)²=4,5π см²