А) Прямые СА1 и АВ1 -скрещивающиеся прямые по определению: "Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости и не имеют общих точек".
Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
Проведем В1С2 параллельно А1С. Тогда <АВ1C2=90° (дано).<br>Соединим точки С и С2, В и С2 => четырехугольник АСС2В - параллелограмм по построению. АС2 и СВ - его диагонали, которые точкой пересечения О делятся пополам.
В прямоугольном треугольнике АВ1С2 отрезок В1О - медиана и В1О=АО=ОС2. Треугольник ОВС2 - прямоугольный, так как В прямоугольном треугольнике ОВ1В (
Вариант с использованием теоремы о трех перпендикулярах: "Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной". Проведем прямую "а" параллельно прямой А1С. Тогда АВ1 перпендикулярна этой прямой, так как она перпендикулярна А1С (дано). Прямая АС1- проекция АВ1 на плоскость грани АА1С1С. Следовательно, АС1 перпендикулярна прямой "а" и перпендикулярна прямой А1С, параллельной прямой "а". Итак, А1С перпендикулярна АС1, а это диагонали прямоугольника АА1С1С. Прямоугольник с перпендикулярными диагоналями - квадрат. АА1=АС, что и требовалось доказать.
б) Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой. Значит нам надо найти расстояние между прямой А1С и плоскостью АВ1С2, которая параллельна прямой А1С по построению так как В1С2 параллельна А1С.
Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.
Геометрическое решение затруднено построением искомого перпендикуляра.
Применим координатный (векторный) метод. Привяжем начало координат к точке С. Тогда имеем точки А(0;6;0), В1(3;0;6), А1(0;6;0) и С(0;0;0).
Вектор АВ1{3-0;0-6;6-0)=АВ1{3;-6;6}, вектор А1С{0-0;0-6;0-6}=А1С{0;-6;-6}. Уравнение прямой АВ1: (Х-0)/3=(У-6)/-6=(Z-0)/6 или Х/3=(У-6)/6=Z/6.
Уравнение прямой А1С: (Х-0)/0=(У-б)/-б=(Z-0)/-б или х/0=(У-6)/-б=Z/-б.
Даны скрещивающиеся прямые АВ1: X/3=(Y-6)/6=Z/6. A1C: X/0=(Y-6)/6=Z/6.
Через прямую AB1 проводим плоскость, параллельную прямой A1C (находим уравнение этой плоскости).
Поскольку прямая АВ1 должна лежать в плоскости , берем точку А, принадлежащую первой прямой, и её направляющий вектор:
А(0;6;0), n1{3;6;6} (координаты направляющего вектора - знаменатели дробей из уравнения прямой).
Находим уравнение плоскости через определитель:
|X-0 3 0| X*| 6 -6| - (Y-6)*| 3 0| + Z*|3 0| =0.
|Y-6 6 -6| |-6 -6| |-6 -6| |6 -6|
|Z-0 -6 -6| =0;
-72X-(Y-6)(-18)+Z(-18)=0 или
4X-Y-Z+6=0 - получили уравнение прямой с коэффициентами
А=4, В=-1, С=-1, D=6.
Расстояние от прямой до плоскости (расстояние от любой точки прямой до этой плоскости) находим по формуле:
d(С;α)=|A*Xc+B*Yc+C*Zc+D|/√(A²+B²+C²), взяв точку С(0;0;0), принадлежащую прямой СА1.
d(C;α)=6/√(16+1+1)=6/3√2=2/√2=√2.
Ответ: искомое расстояние равно √2.
Геометрический способ решения (приложение 2):
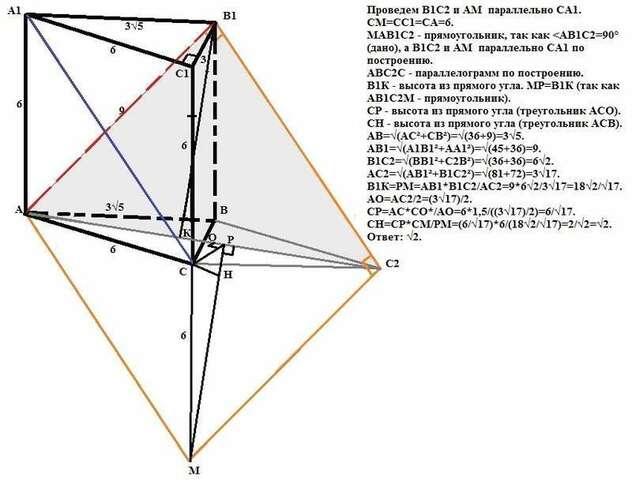
Проведем В1С2 и АМ параллельно СА1.
СМ=СС1=СА=6.
МАВ1С2 - прямоугольник, так как АВС2С - параллелограмм по построению.
В1К - высота из прямого угла. МР=В1К (так как АВ1С2М - прямоугольник).
СР - высота из прямого угла (треугольник АСО).
СН - высота из прямого угла (треугольник АСВ).
АВ=√(АС²+СВ²)=√(36+9)=3√5.
АВ1=√(А1В1²+АА1²)=√(45+36)=9.
В1С2=√(ВВ1²+С2В²)=√(36+36)=6√2.
АС2=√(АВ1²+В1С2²)=√(81+72)=3√17.
В1К=РМ=АВ1*В1С2/АС2=9*6√2/3√17=18√2/√17.
АО=АС2/2=(3√17)/2.
СР=АС*СО*/АО=6*1,5/((3√17)/2)=6/√17.
СН=СР*СМ/РМ=(6/√17)*6/(18√2/√17)=2/√2=√2.
Ответ: √2.