Найдите обьем и полную поверхность треугольной пирамиды, если все боковые ребра равны...

$V= \frac{1}{3} SH$
$S= \frac{1}{2} AC*BC$
По теореме Пифагора
BC=√AB²-AC²=√13²-5²=√169-25=√144=12
S=5*12/2=30
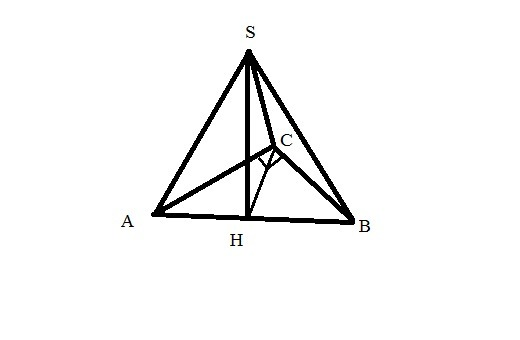
Основание высоты пирамиды - это центр описанной вокруг треугольника ABC, который в прямоугольном треугольнике лежит на середине гипотенузы.
SH=√SA²-AH²=√10²-(6,5)²=√100-42,25=√57,75
V=10√57,75≈76

$S=S_{ABC}+S_{SAB}+S_{SAC}+S_{SBC}\\ S_{ABC}= \frac{1}{2} AC*BC= \frac{1}{2} *5*12=30\\ S_{SAB}= \frac{1}{2} AB*SH= \frac{1}{2} 13* \sqrt{57,75} =6,5 \sqrt{57,75} \\ S_{SAC}= \frac{AC}{4} \sqrt{4SA^2-AC^2} = \frac{5}{4} \sqrt{4*10^2-5^2} = \frac{5}{4} \sqrt{375} = \frac{25}{4} \sqrt{15} \\ S_{SBC}= \frac{BC}{4} \sqrt{4SB^2-BC^2} = \frac{12}{4} \sqrt{4*10^2-12^2} = 3 \sqrt{256} = 3 *16=48\\ S=78+6,5 \sqrt{57,75} +6,25 \sqrt{15}$
S≈151,2