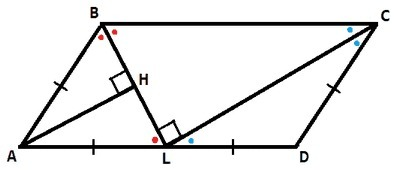
∠ABL=∠LBC (BL - биссектриса ∠ABC)
∠BLA=∠LBC (накрест лежащие углы при AD||BC)
∠ABL=∠BLA => △ABL - равнобедренный (углы при основании равны),
AB=AL
Аналогично CD=LD
AB+CD=AL+LD=AD
AD=BC (ABCD - параллелограмм)
P= AB+BC+CD+AD =3BC
AB=CD => AL=LD (ABCD - параллелограмм)
AD=AL+LD=2AL <=> BC=2AB
∠CLB=90 (биссектрисы углов параллелограмма, прилежащих к одной стороне, перпендикулярны)
AH - высота △ABL, ∠BHA=90
△ABH~△LBC (∠ABL=∠LBC, ∠BHA=∠CLB)
AH/CL=AB/BC=1/2 => AH=CL/2 =12/2=6
S(ABL)= BL*AH/2 <=> BL=2S(ABL)/AH =2*15/6=5
По теореме Пифагора:
BC=√(BL^2 +CL^2) =√(25+144)=13
P=3BC =3*13=39