Решите уравнение. x^2+sqrt(x)-12/x=15

Question

Решите уравнение.
x^2+sqrt(x)-12/x=15

Comments

При x>0 функция x^2-12/x возрастает, а 15-sqrt(x) - убывает, поэтому имеется не более одного решения. х=4 - легко подбирается.

---

х=4, не является корнем!

---

А как тогда быть с этим равенством? :)) 4^2+sqrt(4)-12/4=16+2-3=15

---

ну если так, то да:) я подумал, что x^2+sqrt(x)-12 это числитель

Answer 1

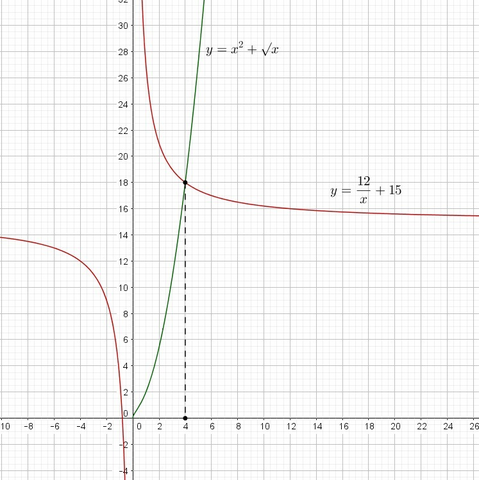
ОДЗ: x>0. Перепишем уравнение в виде x²+√x=12/x+15.
Функция в левой части возрастает на ОДЗ, а функция в правой части - очевидно, убывает. Значит уравнение может иметь не более одного корня. х=4 - легко подбирается: 4²+√4-12/4=16+2-3=15.
На картинке это все изображено на графиках.

---