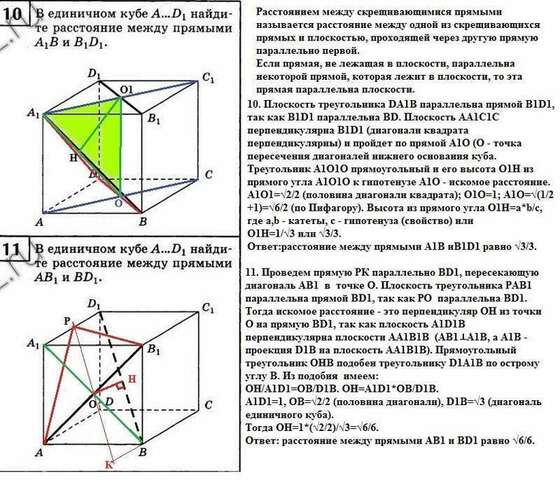
Цитаты: "Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Если прямая, не лежащая в плоскости, параллельна некоторой прямой, которая лежит в плоскости, то эта прямая параллельна плоскости".
10. Плоскость треугольника DA1B параллельна прямой В1D1, так как B1D1параллельна ВD. Плоскость АА1С1С перпендикулярна В1D1 (диагонали квадрата перпендикулярны) и пройдет по прямой А1О (О - точка пересечения диагоналей нижнего основания куба. Треугольник А1О1О прямоугольный и его высота О1Н из прямого угла А1О1О к гипотенузе А1О - искомое расстояние.
А1О1=√2/2 (половина диагонали квадрата); О1О=1; А1О=√(1/2+1)=√6/2 (по Пифагору). Высота из прямого угла О1Н=a*b/c, где а,b - катеты,
с - гипотенуза (свойство) или О1Н=1/√3 или √3/3.
Ответ:расстояние между прямыми А1В иВ1D1 равно √3/3.
11. Проведем прямую РК параллельно ВD1, пересекающую диагональ АВ1 в точке О. Плоскость треугольника РАВ1 параллельна прямой ВD1, так как РO параллельна BD1. Тогда искомое расстояние - это перпендикуляр ОН из точки О на прямую BD1, так как плоскость А1D1В перпендикулярна плоскости АА1В1В (АВ1⊥А1В, а А1В - проекция D1B на плоскость АА1В1В). Прямоугольный треугольник ОНВ подобен треугольнику D1A1B по острому углу В. Из подобия имеем:
ОН/A1D1=OB/D1B. OH=A1D1*OB/D1B.
A1D1=1, OB=√2/2 (половина диагонали), D1B=√3 (диагональ единичного куба).
Тогда ОН=1*(√2/2)/√3=√6/6.
Ответ: расстояние между прямыми АВ1 и ВD1 равно √6/6.