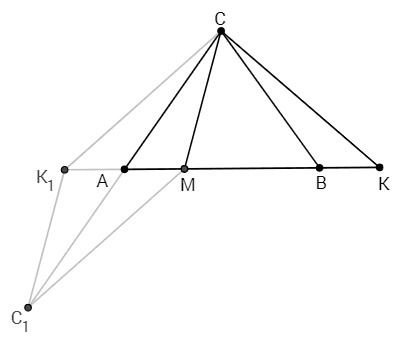
На прямой AB построим отрезок AK1=AM. Треугольник K1CK - равнобедренный (расстояние от точек K1, K до середины отрезка AB равно, медиана и высота из вершины C треугольника ACB является медианой и высотой треугольника K1CK). CK1=CK. AC - медиана треугольника K1CM. Удвоенная медиана меньше суммы сторон из общей вершины. 2AC < CK1+CM <=> AC+BC < CK+CM.
(Докажем, что удвоенная медиана (AC) меньше суммы сторон из общей вершины (CM, CK1). Построим параллелограмм C1K1CM, C1K1=СМ. Диагональ параллелограмма C1C точкой пересечения делится пополам: C1C=2AС. В треугольнике C1K1C сумма двух сторон больше третьей стороны: C1K1+CK1 > C1C <=> CM+CK1 > 2AС)