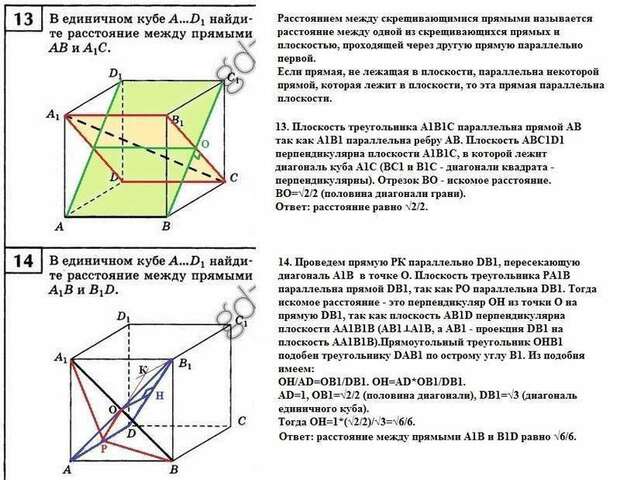
Расстоянием между скрещивающимися прямыми называется расстояние между одной из скрещивающихся прямых и плоскостью, проходящей через другую прямую параллельно первой.
Если прямая, не лежащая в плоскости, параллельна некоторой прямой, которая лежит в плоскости, то эта прямая параллельна плоскости.
13. Плоскость треугольника А1В1С параллельна прямой АВ так как А1В1 параллельна ребру АВ. Плоскость АВС1D1 перпендикулярна плоскости А1В1С, в которой лежит диагональ куба А1С (ВС1 и В1С - диагонали квадрата - перпендикулярны). Отрезок ВО - искомое расстояние. ВО=√2/2 (половина диагонали грани).
Ответ: расстояние между прямыми АВ и А1С равно √2/2.
14. Проведем прямую РК параллельно DВ1, пересекающую диагональ А1В в точке О. Плоскость треугольника РА1В параллельна прямой DВ1, так как РO параллельна DВ1. Тогда искомое расстояние - это перпендикуляр ОН из точки О на прямую DB1, так как плоскость АВ1D перпендикулярна плоскости АА1В1В (АВ1⊥А1В, а АВ1 - проекция DB1 на плоскость АА1В1В). Прямоугольный треугольник ОНВ1 подобен треугольнику DAB1 по острому углу В1. Из подобия имеем:
ОН/AD=OB1/DB1. OH=AD*OB1/DB1.
AD=1, OB1=√2/2 (половина диагонали), DB1=√3 (диагональ единичного куба).
Тогда ОН=1*(√2/2)/√3=√6/6.
Ответ: расстояние между прямыми А1В и В1D равно √6/6.