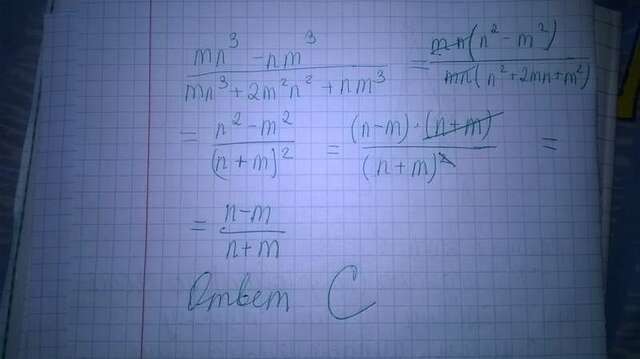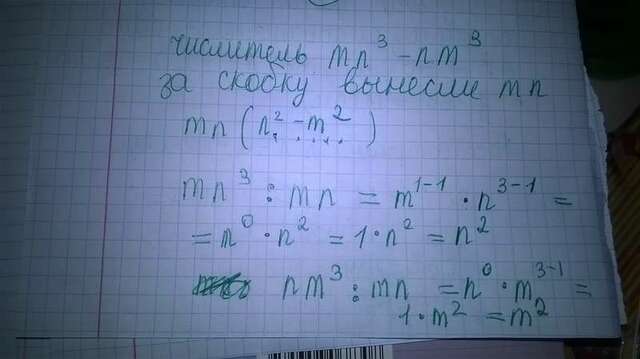♦Решение смотри на фото:
Объяснения:
Читаем вслух выражение ,стоящее в числителе mn³-nm³,что два раза прочитали одно и то же?
Правильно букву n и m
Выбираем в этой строчке (в числителе) буквы с меньшей степенью.Например,есть у нас в числителе есть n³ и n в первой степени,нас интересует n в первой степени.Если в числителе есть m в первой степени и m³,нас интересует меньшая степень и берем m в первой степени.Так вот то ,что прочитали два раза с меньшей степенью выносим за скобку.За скобку выносим mn.
Выражение в скобке определяем делением (смотри фото),при деление основание остается прежнем,а показатели степеней вычитаются.
***число или буква в нулевой степени равна 1.
В скобке у нас получилось n²-m²
В знаменателе проводим такую же операцию за скобку выносим mn,в скобке после деления окажется n²+2mn+m²,а это формула есть такая
(а+b)²=a²+2ab+b²,понятно,что наше выражение n²+2mn+m²=(n+m)²
Итого:мы получаем в числителе mn*(n²-m²),в знаменателе mn*(n+m)².
В числителе и в знаменателе сокращаем одинаковое выражение nm,и у нас остается в числителе (n²-m²),в знаменателе (n+m)².
Работаем с числителем
Есть такая формула
а²-b²=(a-b)*(a+b),ясно,что n²-m²=(n-m)*(n+m)
В числителе теперь у нас (n-m)*(n+m),в знаменателе (n+m)²
Мы сокращаем (n+m) и (n+m)²
Понятно,что (n+m)²=(n+m)*(n+m)
Итак,получается
(n-m)* (n+m)/(n+m)*(n+m)
В числителе и знаменателе сокращаем одинаковое выражение n-m,так как (n-m):(n-m)=1,это как при деление одинаковых чисел например 5:5=1.
После сокращения остается n-m/n+m
♦ Ответ С