Центр тяжести треугольника находится в точке пересечения его медиан. которые всегда пересекаются в одной точке.
Расстояние от точки до плоскости измеряется длиной проведенного от точки до плоскости перпендикулярного отрезка.
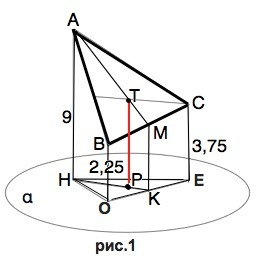
Сделаем рисунок
АН=9, ВО=2,25, СЕ=3,75. Все три отрезка перпендикулярны плоскости альфа.
Проведем в ∆ АВС две медианы, точка пересечения которых - центр тяжести треугольника.
Обозначим АМ медиану из А. Точку пересечения медиан из А и С обозначим Т. Эта точка – центр тяжести ∆ АВС и проецируется в точку Р пересечения медиан ∆ НОЕ– проекции треугольника АВС на плоскость α.
Четырехугольник OВСЕ - прямоугольная трапеция. МК - ее средняя линия, т.к. ВМ=МС, ОК=КЕ.
МК=(2,25+3,75):2=3
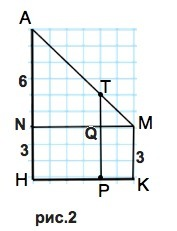
Четырехугольник АНКМ - прямоугольная трапеция. ( см. рис.2)
Медианы треугольника точкой пересечения делятся в отношении 2:1, считая от вершины, ⇒ АТ:ТМ=2:1.
Проведем MN║КН.
AN=AH-MK=9-3=6
∆ АNM ~∆TQM, k=AM:TM=3:1 ⇒
AN:TQ=3:1
3•TQ=6⇒
TQ=2
TP=TQ+QP=2+3=5 (ед. длины) - это ответ.