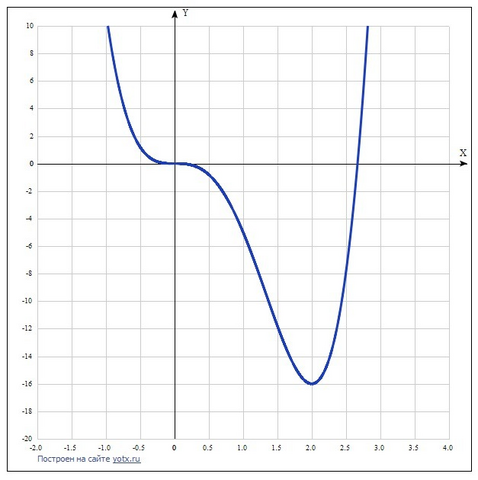
Точки экстремума функции y=3x^4-8x^3 находим, приравняв производную функции нулю:
y' = 12x³ - 24x² = 0.
12x²(x - 2) = 0.
Пока найдены только две критические точки при х = 0 и х = 2.
Для определения экстремумов надо определить изменение знака производной при переходе через критические точки.
x = -1
0 1 2 3
y' = -36 0 -12 0 108.
При переходе через 0 знак производной не меняется, значит это не точка экстремума.
Остаётся 1 точка экстремума - это минимум функции в точке х = 2.