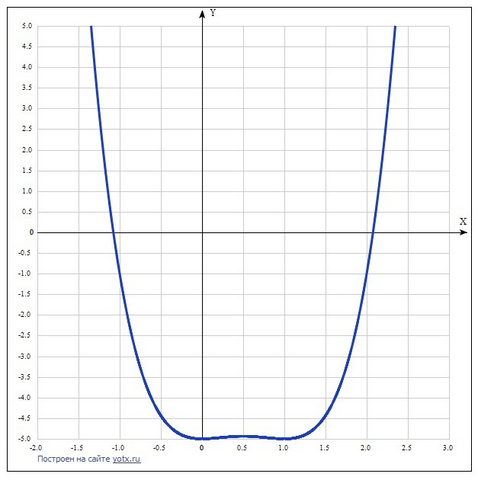
Дана функция у = x^4-2x^3+x^2-5.
Промежутки возрастания и убывания функции определяются её производной.
Где
производная положительна - функция возрастает, где отрицательна - там убывает.
Точки, в которых происходит смена знака - это точки экстремума.
Находим производную и приравниваем её нулю:
y' = 4x³ - 6x² + 2x = 0.
х(4х² - 6х + 2) = 0.
Первый корень - х₁ = 0.
Нулю может быть равен и квадратный трёхчлен:
4х² - 6х + 2 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-6)^2-4*4*2=36-4*4*2=36-16*2=36-32=4;Дискриминант больше 0, уравнение имеет 2 корня:
x₂ = (√4-(-6))/(2*4)=(2-(-6))/(2*4)=(2+6)/(2*4)=8/(2*4)=8/8 = 1;x₃ = (-√4-(-6))/(2*4)=(-2-(-6))/(2*4)=(-2+6)/(2*4)=4/(2*4)=4/8 = 0,5.
Найдены 3 точки, в которых производная равна 0.
Теперь определяем знаки производной в промежутках между этими точками.
x =
-1 0
0,2
0,5 0,7
1 2
y' = -12
0 0,192
0 -0,168
0
12.
Отсюда видим:
функция убывает x ∈ (-∞; 0) ∪ (0,5; 1),
возрастает x ∈ (0; 0,5) ∪ (1; +∞).