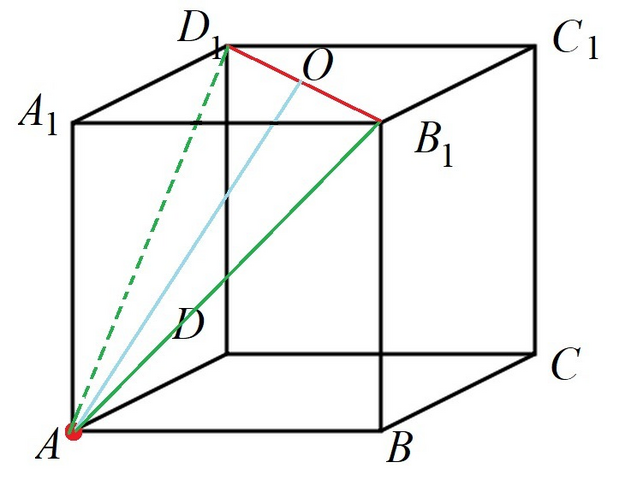
Расстояние между точкой и прямой измеряется по перпендикуляру.
Проведём AO - перпендикуляр к B1D1. Рассмотрим треугольник AB1D1.
AB1 = AD1 - диагонали граней куба, поэтому треугольник равнобедренный с основанием B1D1.
AO - высота, проведенная к основанияю, поэтому AO - медиана.
ΔA1B1D1 - прямоугольный. По теореме Пифагора B1D1^2 = A1B1^2 + A1D1^2, B1D1^2 = 2.
Аналогично, AB1^2 = 2.
В1О = 1/2 B1D1, B1O^2 = 1/2.
ΔAB1O - прямоугольный, по теореме Пифагора AO^2 + B1O^2 = AB1^2.
AO^2 = AB1^2 - B1O^2 = 2 - 1/2 = 3/2 = 6/4
AO = √(6/4) = √6 / 2
Ответ. √6 / 2.