Одним из методов решения задач на построение является метод геометрических мест.
Геометрическим местом точек называется фигура, которая состоит из всех точек плоскости, обладающих определенным свойством.
Например, окружность можно определить как геометрическое место точек, равноудаленных от данной точки.
Важное геометрическое место точек дает следующая теорема:
Геометрическое место точек, равноудаленных от двух данных точек, есть прямая, перпендикулярная к отрезку, соединяющему эти точки, и проходящая через его середину.
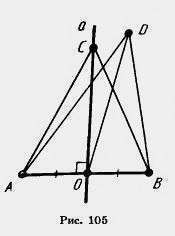
Доказательство. Пусть А к В — данные точки, а — прямая, проходящая через середину О отрезка АВ перпендикулярно к нему (рис. 105). Мы должны доказать, что:
1) каждая точка прямой а равноудалена от точек А и В;
2) каждая точка D плоскости, равноудаленная от точек А к В, лежит на прямой а.
То, что каждая точка С прямой а находится на одинаковом расстоянии от точек А и В, следует из равенства треугольников АОС и ВОС. У этих треугольников углы при вершине О прямые, сторона ОС общая, а АО=ОВ, так как О — середина отрезка АВ.
Покажем теперь, что каждая точка D плоскости, равноудаленная от точек А и В, лежит на прямой а. Рассмотрим треугольник ADB. Он равнобедренный, так как AD = BD. В нем DO — медиана. По свойству равнобедренного треугольника медиана, проведенная к основанию, является высотой. Значит, точка D лежит на прямой а. Теорема доказана.