100 баллов. Геометрия. Решить 9.349 подробно. Неверное и нерасписанное удаляется...

Question

100 баллов. Геометрия. Решить 9.349 подробно. Неверное и нерасписанное удаляется админами, таковы здесь правила.

---

Comments

Скучная задача. Их теоремы Менелая находится CN/CD = 2/3; там надо пролить боковые стороны до пересечения в точке F и считать BN секущей для треугольника AFC; отсюда уже элементарно найти Scon/Scad = 2/9; а Scad = (3/5)Sabcd; ну где то так, возможно я в числах где то ошибся, проверьте. Мне лень считать всё это, пусть кто-то другой оформит как положено и получит очки, я не против. Время ставлю, чтобы спамеры не лезли. 08.06.2017 16:33

---

Тут самое проблемное - именно применение теоремы Менелая. Ни слова о ее при менении вы не сказали

---

Нет, Менелая пока что в белорусских школах даже на повышенном уровне не проходим, её нет ни в программе, ни в выпускных экзаменах, ни в тестировании при прохождении в вуз. Но за решение всё равно спасибо.

---

Постарался очень подробно записать.

---

cos20093 прав, задачка нудноватая. Но ssoxo решил ее нескучно. Однако, ее все же, видимо надо решать по Менелаю (тему проходите?). На всяк прилагаю решение http://prntscr.com/fhtgr3

---

если решенме есть, почему, написав на листочке, на даёте в ответ?

---

Как не сказал? :( Треугольник AFC, секущая BN, (AB/BF)*(FN/NC)*(CO/OA) =1; а из BC/AD = 2/3; получается AB/BF = 1/2 (ну потому что AF/BF = AD/BC) отсюда CN = FN/4; или 4*CN = FC + CN; 3*CN = FC = 2*CD; (опять таки потому что FD/CD = AD/BC); как же не сказал?

Answer 1

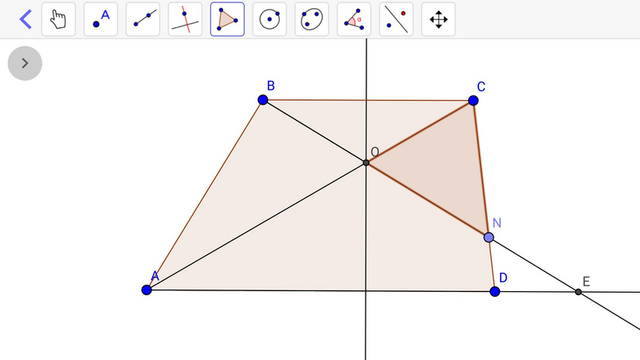
Не нужно никакого Менелая.

Сделаем дополнительное построение как на рисунке.
Как известно, треугольники АОЕ и ВОС подобны с коэффициентом подобия k=АО:ОС=2:1. Такое же отношение имеют их высоты. Высота тр-ка ВОС равна h, а высота трапеции, соответственно, 3h. 
Так как ВС:АЕ=1:2=2х:4х и ВС:АД=2х:3х, то ДЕ=1х.
Треугольники ВСN и NED подобны по трём углам. ВС:ДЕ=2:1, значит высота тр-ка ВСN равна 2h.

S(ВОС)=2х·h/2=xh,
S(BCN)=2x·2h/2=2xh,
Разность этих площадей даст S(CON)=xh.

S(ABCD)=(2x+3x)·3h/2=7.5xh.

Итак, S(CON):S(ABCD)=xh:7.5xh=2:15 - это ответ.

---

Comments

Упростили, победили в массовости, но проиграли в качестве, можно сказать. Такой уж путь развития у неё. По средствам. Конечно, от государства зависит, чему будут учить в бесплатных для всех школах стран СНГ, в основном.

---

Спасибо всем за комментарии. Могу лишь добавить, что беда не только у андроид-версии сайта. В версии для iOS те же проблемы, а может и хуже. Помимо прочего, отсутствует возможность использования дополнительной клавиатурой со специальными символами, что сильно затрудняет написание ответов.

---

спасибо

---

я передам Вашу информацию администрации

---

а)в андроид-версии не видна в списке заданий его цена в баллах б)в андроид не видно больше 1 фото к заданию или ответу. и добавить тоже нельзя в)в моб.браузере нельзя выбрать несколько дисциплин сразу по поиску вопросов г)теперь с нововведннием из-за галочки 《проверено экспертами》 вообще не видно в андроид-версии, ответ помечен как луший или нет

---

неотвечающие разработчики андроид и становящееся хуже приложение заставляют его удалить:

---

Мне вот давно интересно. Кто-нибудь ругает администраторов за то, что андроид-версия уступает просто мобильной версии браузера? Я, кроме себя, никого тут таких не видел. С каждым днём она не лучше, а только хуже. Задумка сервиса Знания.ру великолепна, но из-за оформления андроид-версии я её, пожалуй, удалю и перейду просто на мобильную версию браузера, потому что невыносимо уже:

---

Большое спасибо. Все мнения было интересно почитать. Правда, я не думаю, что система образования 《скатилась》, она просто на начальных, школьных, этапах хочет засунуть в головы учеников больше информации, чем может досконально и понятно объяснить. И это далеко не лучший вариант. С другой стороны, она победила в массовости. Теперь для решения задач по физике, математике и даже каких-то языковых вопросов люди не проводят анализ, а просто вспоминают заученное правило.

---

Жаль что система образования "скатилась" до "произвести некоторые действия, не требующие включения "соображательной части" мозга... " Мне всегда импонируют как раз нетрадиционные подходы к решению.. в обход "навязанного данной темой решения"... Если есть желание решить нетрадиционно.. могу повторить эти задачи https://znanija.com/task/20060432 https://znanija.com/task/20060145 https://znanija.com/task/20059521 решения, которые есть дала моя дочь..

---

Я понимаю, что можно скачать на устройство мобильную научную клавиатуру и использовать её, но адекватная версия стоит денег, а сайт позиционирует себя как бесплатное приложение и навязывать платные услуги ему как-то не к лицу. Подумаем над этим.