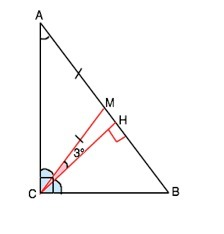
Медиана прямоугольного треугольника, проведенная к гипотенузе, равна её половине, и делит треугольник на два равнобедренных.
Обозначим треугольник АВС, медиану СМ, высоту – СН.
В равнобедренном ∆ АМС стороны АМ=СМ, ∠САМ=∠МСА.
Высота прямоугольного треугольника, проведенная к гипотенузе, делит его на подобные треугольники.
∠ВСН=∠САВ. ⇒ ∠ВСН=∠МСА.
Угол АСВ=2∠АСМ+∠МСН
90°-3°=2АСМ ⇒
∠АСМ=43,5°
Второй острый угол равен 90°-43,5°=46,5° - это искомый больший угол.