ДАНО
Y(х) = 0.2*x⁵ - 0.5*x² + 2.7.
РЕШЕНИЕ
Находим производную функции.
Y'(x) = 0.2*5*x⁴ - 0.5*2*x = x⁴ -x = x³*(x - 1)
Находим корни производной - точки экстремумов - Y'(x) = 0.
х1 = 0 - максимум - Y(0) = 2.7
х2 = 1 - минимум - Y(1) = 2.4
Интервалы монотонности
Возрастает - Х∈(-∞;0]∪[1;+∞) - производная положительная
Убывает - Х∈[0;1] - производная отрицательная.
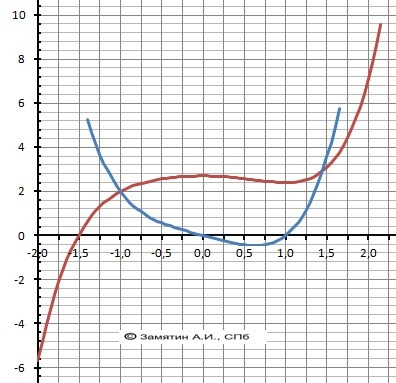
График функции и производной - в приложении.