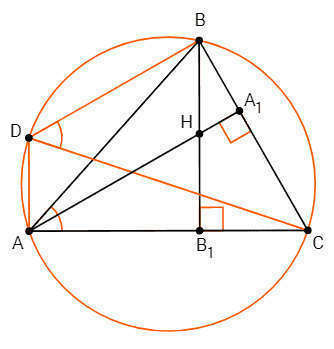
Построим параллелограмм ADBH: DA||BB1, DB||AA1
DB=AH
∠DAC=∠BB1C=90, ∠DBC=∠AA1C=90 (соответственные углы при параллельных).
Около ADBC можно описать окружность (сумма противолежащих углов равна 180).
∠BDC=∠BAC (вписанные углы, опирающиеся на хорду BC)
BC/DB =tg(BDC) <=> BC/AH =tg(BAC)