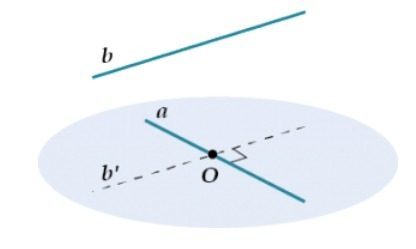
Первое, - прямые, лежащие в разных плоскостях, могут быть перпендикулярны друг другу, не пересекаясь при этом. - рис.1
Для доказательства - построим прямую b' || b и принадлежащую плоскости, в которой находится прямая а.
Если b'⊥a, то и b⊥a.
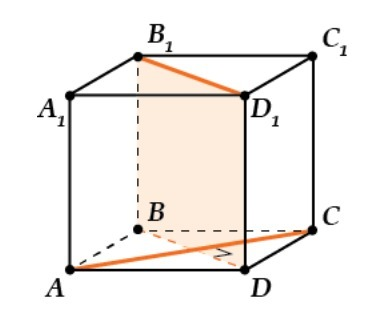
Второе, - простейшая иллюстрация условия задачи - куб (рис.2)
Пусть дан куб ABCDA₁B₁C₁D₁.
Необходимо найти угол между скрещивающимися прямыми АС и B₁D₁.
Проведем BD.
Так как BB₁D₁D - прямоугольник, отсюда следует, что B₁D₁ || BD.
Так как ABCD - квадрат, => AC⊥BD => AC⊥B₁D₁