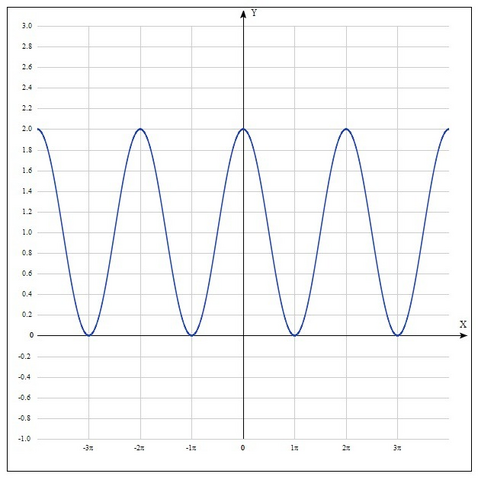
Y = 1 +cosx
1) E(y) = [0; 2]
2) D(y) = (-∞; +∞)
3) Функция периодическая. Основной период равен 2π.
4) y = f(x)
График функции симметричен относительно оси Oy, функция является чётной.
5) Пересекается с осью Oy в точке (0; 2).
С осью Oy периодично пересекается в точке π + 2πn, n ∈ Z.
5) Асимптот у функции нет
6) Т.к. функция периодическая, то рассмотрим её на отрезке [-π; π].
Найдём производную функции:
y' = -sinx
-sinx ≥ 0
sinx ≤ 0
x ∈ [-π; 0]
Значит, на [-π; 0] функция возрастает, а на [0; π] убывает.
7) ymin = 0
ymax = 2
8) Точек экстремума у функции нет.
9) Таблица точек:
x -π -π/2 0 π/2 π
y 0 1 2 1 0