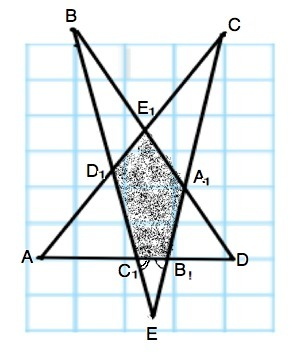
Пятиконечная звезда построена на продолжении сторон выпуклого пятиугольника. Найдите сумму углов ∠А, ∠В, ∠С, ∠D и ∠Е, если А1В1С1D1Е1 - выпуклый пятиугольник.
Применим теорему о внешнем угле треугольника: Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Угол С1В1Е - внешний угол ∆ АСВ1 и равен ∠А+∠С;
угол ЕС1В1 - внешний угол ∆ С1ВD и равен ∠В+∠D
Тогда сумма углов - вершин "лучей" звезды
∠Е+(∠А+∠С)+(∠В+∠D)=∠Е+∠ЕВ1С1+∠ЕС1В1=180°