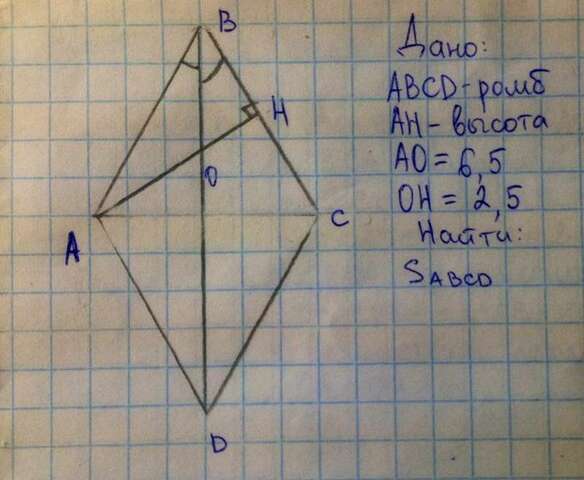
1) Рассмотрим прямоугольные ΔОВН и ΔАOD.
∠ОВН = ∠ADO (BD - биссектриса углов В и D) ⇒ ΔОВН ~ ΔАOD.
2) Пусть ВН = х. Тогда по теореме Пифагора в прямоугольном ΔАВС
АВ² = ВН² + АН²
АВ² = х² + (6,5 + 2,5)²
АВ = √(х² + 9)
3) Т.к ΔОВН ~ ΔАOD, то BH/AD = OH/AO.
AB = AD
x / √(x² + 9) = 2,5 / 6,5
2,5√(х² + 9) = 6,5х
Возводим уравнение в квадрат:
6,25 (х² + 9) = 42,25х²
6,25х² + 56,25 - 42,25х² = 0
- 36х² + 56,25 = 0
36х² - 56,25 = 0
D = 0² - 4 * 36 * (- 56,25) = 8100
x₁ = (0 + √8100) : (2 * 36) = 90 : 72 = 1,25
x₂ = (0 - √8100) : (2 * 36) = (- 90) : 72 = - 1,25
ВН = 1,25
4) АВ = √(1,25² + 9) = √(1,5625 + 9) = √10,5625 = 3,25
AB = BC = 3,25
5) SABCD = AH * BC = 9 * 3,25 = 29,25
Ответ: 29,25 ед.²