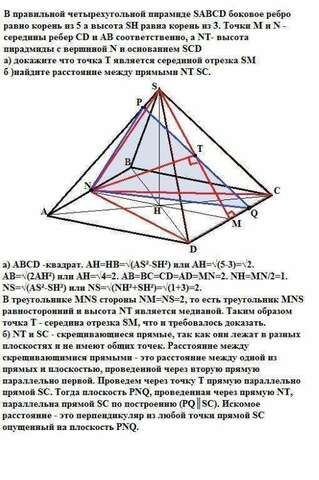
А) ABCD -квадрат. АН=НВ=√(AS²-SH²) или АН=√(5-3)=√2.АВ=√(2АH²) или АН=√4=2. АВ=ВС=СD=AD=MN=2. NH=MN/2=1.NS=√(AS²-SH²) или NS=√(NH²+SH²)=√(1+3)=2.
В треугольнике MNS стороны NM=NS=2, то есть треугольник MNS равносторонний и высота NT является медианой. Таким образом точка Т - середина отрезка SM, что и требовалось доказать.
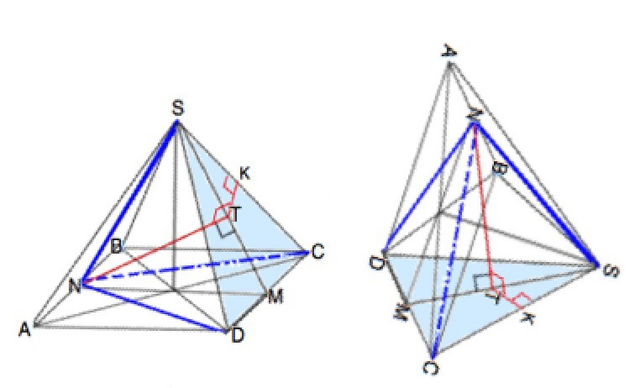
б) NT и SС - скрещивающиеся прямые, так как они лежат в разных плоскостях и не имеют общих точек. Расстояние между скрещивающимися прямыми - это расстояние между одной из прямых и плоскостью, проведенной через вторую прямую параллельно первой. Проведем через точку Т прямую параллельно прямой SC. Тогда плоскость PNQ, проведенная через прямую NT, параллельна прямой SC по построению (PQ║SC). Искомое расстояние - это перпендикуляр из любой точки прямой SC опущенный на плоскость PNQ.
Рассмотрим пирамиду NCDS (приложение 2). Перпендикуляр ТК к стороне SC - нужное расстояние, т.к. NT перпендикулярна плоскости CDS, значит, и любой прямой, проходящей через Т. Получили подобные ∆ MCS и KTS по острому углу S. Тогда КТ/МС=ST/SС. Отсюда искомое расстояние ТК=ST*MC/SC.
НайдемSM по Пифагору: SM=√(SC^2-CM^2) или SM=√(5-1)=2. ST=SM/2 или ST=1.TK=1*1/√5=√5/5. Это ответ.