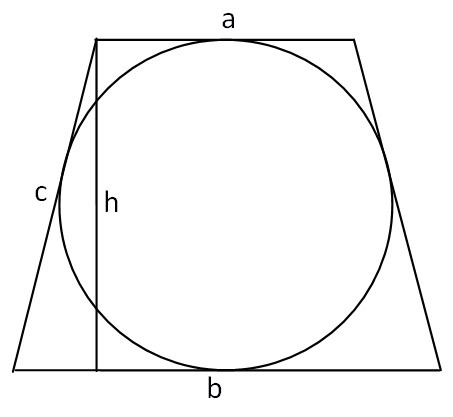
Если обозначить диаметр окружности через d,d, то нужно получить, что d=ab−−√.d=ab.
Так как окружность вписана в трапецию, то c+c=a+b⇒c=a+b2.c+c=a+b⇒c=a+b2.
По теореме Пифагора из треугольника на рисунке запишем h2=c2−(a−b2)2=(a+b2)2−(a−b2)2==(a+b2−a−b2)(a+b2+a−b2)=2b2∗2a2=ab.h2=c2−(a−b2)2=(a+b2)2−(a−b2)2==(a+b2−a−b2)(a+b2+a−b2)=2b2∗2a2=ab.
Заметим, что d=h.d=h. Тогда окончательно получим d2=ab⇒d=ab−−√.d2=ab⇒d=ab.
Ответ доказано.