Устная задача... за 50 баллов)))
1) отрезки касательных, проведенных из одной точки к окружности, равны.
2) радиус, проведенный в точку касания, перпендикулярен касательной.
3) центр вписанной в угол окружности лежит на биссектрисе этого угла.
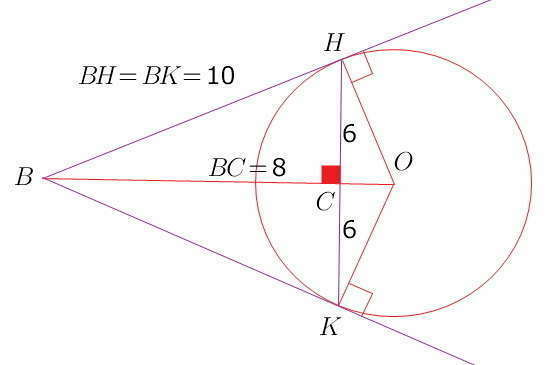
здесь всегда получаются два абсолютно равных прямоугольных треугольника ВОН и ВОК
легко доказывается, что и треугольники ВСН и ВСК тоже абсолютно равные и прямоугольные... (по двум сторонам BH=BK, BC-общая и углу между ними: ВО-биссектриса)))
ВНК равнобедренный и СН=СК ---> ВС _|_ НК
треугольник ВСН (ВСК) - египетский (подобен треугольнику со сторонами 3; 4; 5) его стороны 6; 8; 10