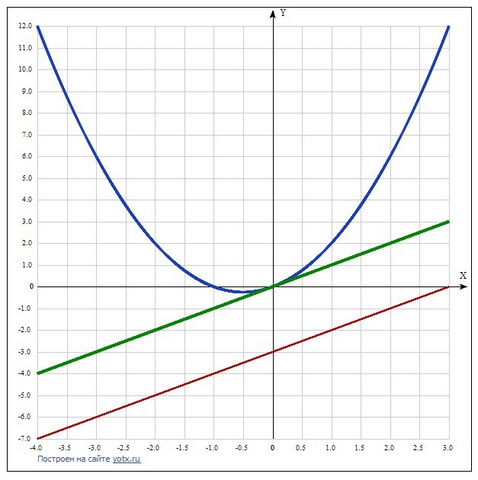
Дана функция y=x^2+x и прямая, параллельная касательной, y=x-3.
Коэффициент к в уравнении касательной равен производной функции.
Из задания следует, что к = 1.
Производная: y' = 2x + 1 равна 1:
2х + 1 = 1,
2х = 0,
х = 0 это координата точки касания, то есть прямая с коэффициентом при х, равным 1, проходит через начало координат.
Получаем уравнение касательной у = х.