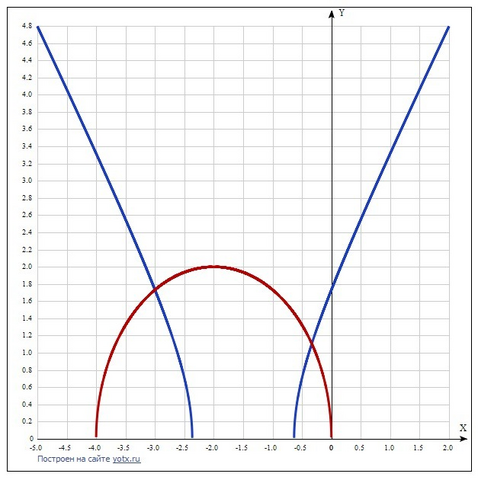
Сначала находим область определения функций.
f(x) = √(2x² +6x + 3).
Подкоренное выражение должно быть больше или равно нулю.
2x² +6x + 3 ≥ 0.
Квадратное уравнение 2x² +6x + 3 = 0, решаем относительно x: Ищем дискриминант:
D=6^2-4*2*3=36-4*2*3=36-8*3=36-24=12;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√12-6)/(2*2)=(√12-6)/4=√12/4-6/4=√12/4-1,5 ≈ -0,633975; x₂=(-√12-6)/(2*2)=(-√12-6)/4=-√12/4-6/4=-√12/4-1,5 ≈ -2,366025.
То есть, для этой функции -∞ < x < -2,366025 и х > -0,633975.
Для второй функции -х² - 4х ≥ 0,
-х(х+4) ≥ 0 имеем 2 крайних значения x < 0 и x > -4.Так как подкоренные выражения положительны, первое из них больше или равно второму.
2х² + 6х + 3 ≥ - х² - 4х ,
2х² + 6х + 3 + х² + 4х ≥ 0,
3х² + 10х + 3 ≥ 0.
Решаем квадратное уравнение 3х² + 10х + 3 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=10^2-4*3*3=100-4*3*3=100-12*3=100-36=64;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√64-10)/(2*3)=(8-10)/(2*3)=-2/(2*3)=-2/6=-(1/3) ≈ -0.33333; x₂=(-√64-10)/(2*3)=(-8-10)/(2*3)=-18/(2*3)=-18/6=-3.
Объединение полученных областей даёт ответ:
-4 ≤ x ≤ -3, (-1/3) ≤ x ≤ 0.