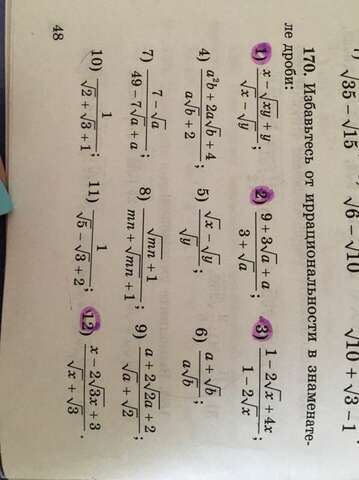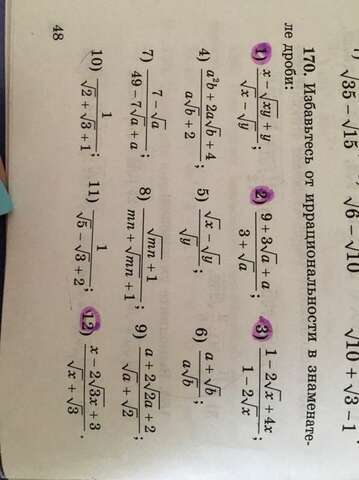Избавтесь от иррациональности в знаменателе дроби, срочно нужно! Буду очень благодарен
1.) x-√xy+y
-----------
√x-√y
2.) 9+3√a+a
------------------
3+√a
3.) 1-2√x+4x
-----------------
1-√2x
12.) x-2√3x+3
-------------------
√x+√3
Заранее благодарен