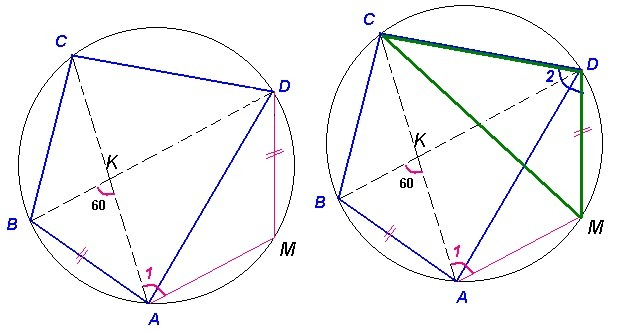
Четырёхугольник ABCD со сторонами AB=43 и CD=4 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60∘. Найдите радиус окружности, описанной около этого четырёхугольника.
проводим АМ параллельное ВD следовательно DМ=АВ (почему ???? как к этому пришли) + по противолежащим находим угол 2 и в треугольнике СDМ по теореме сначала косинусов потом синусов находим радиус
но вот обоснуйте откуда DМ=АВ, или другое решение , пожалуйста