1)
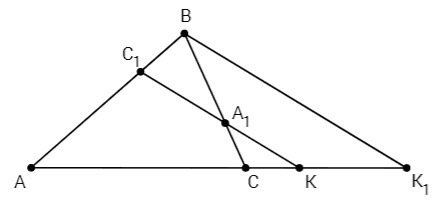
BK1||C1A1
Параллельные прямые отсекают на секущих пропорциональные отрезки (теорема Фалеса).
AK/KK1 =AC1/C1B =5/2
CK/KK1= A1C/BA1 =1/2
AK/CK =5 <=> (AC+CK)/CK =5 <=> AC/CK +1 =5 <=> СK/АС =1/4
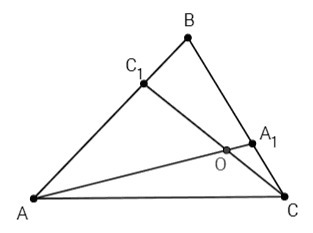
2)
BA1= 2*A1C
BC= 3*A1C
AC1= 2,5*C1B
AB=3,5*C1B
∠COA1=∠C1OA (вертикальные углы)
sin(CC1B)= sin(180-AC1C) =sin(AC1C)
По теореме синусов:
C1B/sin(BCC1) = BC/sin(CC1B) <=> sin(CC1B)= BC*sin(BCC1)/C1B
AO/sin(AC1C) = AC1/sin(C1OA) <=> AO= AC1*sin(AC1C)/sin(C1OA)
OA1/sin(BCC1) = A1C/sin(COA1) <=> OA1= A1C*sin(BCC1)/sin(C1OA)
AO/OA1= AC1*sin(AC1C)/A1C*sin(BCC1) = 2,5*C1B*3*A1C*sin(BCC1)/A1C*C1B*sin(BCC1) =7,5
sin(BA1A)= sin(180-AA1C) =sin(AA1C)
sin(A1AB)= BA1*sin(BA1A)/AB
CO= A1C*sin(AA1C)/sin(COA1)
OC1= AC1*sin(A1AB)/sin(C1OA)
CO/OC1= A1C*sin(AA1C)/AC1*sin(A1AB) = A1C*3,5*C1B*sin(BA1A)/2,5*C1B*2*A1C*sin(BA1A) =0,7