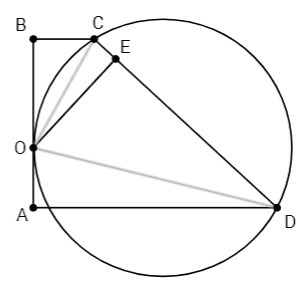
Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой хордой.
∠BOC= 1/2 U OC
Вписанный угол равен половине дуги, на которую опирается.
∠ODE= 1/2 U OC
∠BOC=∠ODE => △BOC~△ODE (прямоугольные т. с равными острыми углами)
OC/OD=BC/OE
Аналогично ∠OCE=∠AOD => △OCE~△AOD
OC/OD=OE/AD
BC/OE=OE/AD <=> OE= √(BC*AD) =√(12*48) =24
-------------------------------------------------------------------------------------------------------
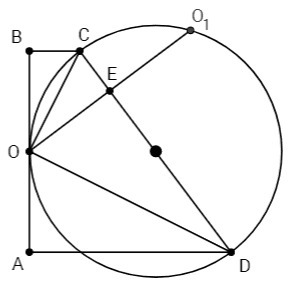
P.S. Частный случай, когда центр окружности находится на CD:
△BOC=△OCE (диаметр, перпендикулярный к хорде, делит хорду и стягиваемые ею дуги пополам: U OC=U CO1, ∠BOC=COE), △AOD=△ODE, BC=CE, AD=ED. Вписанный угол, опирающийся на диаметр, прямой. ∠COD=90. Высота, проведенная из вершины прямого угла, равна среднему геометрическому проекций катетов на гипотенузу. OE= √(CE*ED) = √(BC*AD).