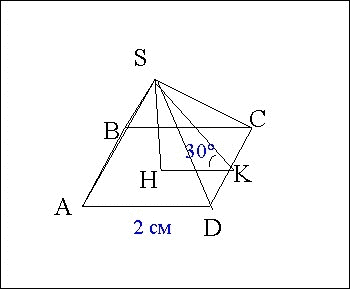
Дано:
пирамида SАВСД
АВ=ВС=СD=АD=2см
высота SН=6см
∠SКН = 30°
Найти Sполн. пирамиды АВСD
Решение
1) В прямоугольном Δ SНК катет SН = 6 см лежит против угла в 30°, значит, он равен половине гипотенузы SК.
Отсюда гипотенуза SК = 2SН=2*6см = 12 см.
2) Площадь боковой поверхности состоит из 4-х одинаковых треугольников.
Найдём S₁ - площадь ∆SDС, одного из этих четырёх, а затем
умножим на 4.
S бок = 4S₁ = 4 * 1/2 * DС * SК = 2 * 2 см * 12 см= 48 см²
3) S осн = Sквадрата = 2 см * 2 см = 4 см²
4) S полн. = S бок + S осн = 48 см² + 4 см² = 52 см²
Ответ: 52 см²