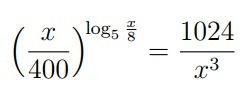Есть идеи как решить?
1) пытался логарифмировать обе части
2) приводить к одному основанию степени
В итоге остается куча логарифмов, из-за которых не могу решить квадратное уравнение, к которому сводится решение.
В итоге не получается ничего.
Возможно, решается очень легко, но я не могу найти решение.
Ответ известен (два корня): 8/5, 16